yade-dev team mailing list archive
-
 yade-dev team
yade-dev team
-
Mailing list archive
-
Message #06731
Re: Another stress in bodies
Thanks, Bruno!
I will have a look at this, but, please, do not delete the previous
function, it is used in VTKRecorder.
Anton
On Mon, Jan 17, 2011 at 6:44 PM, Bruno Chareyre
<bruno.chareyre@xxxxxxxxxxx>wrote:
> X <#12d951324e8b01b3_>LatexIt! run report...
>
> *** Found expression $$\sigma_{ij}^{macro}/compacity$$
> Image was already generated
> *** Found expression $$\int_V s_{ij}dV = \int_{S_V} x_i.s_{ij}.n_j.dS = \sum_kx_i^k.f_j^k$$
>
> Hi,
>
> I've been adding another definition of stress in particles (not adapted to
> periodic BCs yet, though not difficult).
> For those interested. The documentation is pasted below.
> _____________
> Compute the exact mean stress tensor in each sphere from the contour
> integral of applied load.
> After divergence theorem, at equilibrium:
> [image: $$\int_V s_{ij}dV = \int_{S_V} x_i.s_{ij}.n_j.dS =
> \sum_kx_i^k.f_j^k$$].
> This relation applies for arbitrary shapes but the result has to be divided
> by the solid's volume, computed here using the radii, hence assuming
> spheres. The (weighted) average of per-body stresses is exactly equal to the
> average stress in the solid phase, i.e. [image:
> $$\sigma_{ij}^{macro}/compacity$$].
> _____________
>
> Cheers.
>
> Bruno
>
>
> _______________________________________________
> Mailing list: https://launchpad.net/~yade-dev
> Post to : yade-dev@xxxxxxxxxxxxxxxxxxx
> Unsubscribe : https://launchpad.net/~yade-dev
> More help : https://help.launchpad.net/ListHelp
>
>
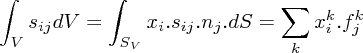
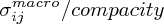
Follow ups
References